آزمون مانتل (Mantel test ) چیست

 در سال 1967 مانتل آزمون نسبتاً مفيدي را براي مقايسه دو ماتريس فاصله، به عنوان راه‌حلي جهت تشخيص گروه‌بندي بيماري‌ها از لحاظ مكاني و زماني معرفي كرد (Mantel. 1967).

 آزمون مانتل به منظور تعيين ارتباط ميان دوماتريس فاصله مستقل از هم كه هر دو يك گروه از مشاهدات را در برمي‌گيرند، استفاده مي‏شود. آزمون صفر فرضيه مانتل عدم ارتباط ميان اعضاي يك ماتريس با اعضاي ماتريس ديگر است لذا معني‌دار شدن اين آزمون نشان‌دهنده وجود ارتباط ميان دو ماتريس مي‌باشد.

       براي انجام آزمون مانتل از آماره‌ي z استفاده مي‏شود كه از رابطه زير به دست مي‌آيد:

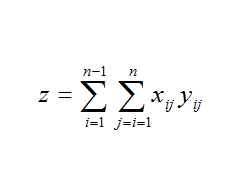
كه در آن xij و yij به ترتيب اجزاي دو ماتريس x, y مي‌باشند كه به حاصلضرب آن‏ها، محصول هادامارد^[1] دو ماتريس گفته مي‏شود . اگر فواصل دو ماتريس در ارتباط با هم باشند مقدارz از حد متوسط بالاتر مي‌رود و بالعكس اگر ارتباط منفي بين دو ماتريس باشد يعني مقادير بالاي xij با مقادير پايين yij و برعكس ارتباط داشته باشد، مقدار z كوچك مي‏شود.

 آزمون اينكه z بدست آمده از لحاظ آماري معني‌دار و يا غيرمعني‌دار مي‌باشد، توسط آزمون تصادفي كردن^[2] انجام مي‌‌گيرد. در اين آزمون عناصر ماتريس‌ها نسبت بهم بطور تصادفي جابجا مي‌شوند كه به اين عمل چپگشت يا فراگردي^[3] گفته مي‏شود.

 آماره‌ي z معمولاً به صورت واحد آزاد^[4] استفاده مي‏شود و فهم كاربر آن بدون آزمون معني‌دار بسيار مشكل است. به همين دليل از ضريب مانتل استاندارد شده استفاده مي‏شود كه ضريب همبستگي ميان اجزاي دو ماتريس[5] مي‌باشد. با اين وجود نمي‌توان از آزمون معني‌دار بودن رايج براي ضريب همبستگي در اين مورد استفاده نمود زيرا عناصر ماتريس‌هاي مطالعه شده، آنچنانكه در تئوري ضريب همبستگي مطرح است، مشاهدات دو متغير مستقل نمي‌باشند. به همين علت بجاي آن مي‌بايد تعداد بالايي جابجايي تصادفي در رديف‌ها و ستون‌هاي يك ماتريس را انجام داد و در هر بار تغيير ضريب همبستگي را محاسبه نمود و اين ضريب را با سطح آماري موردنظر، بعنوان مثال 95%، مقايسه كرد.

 از اين نتايج مي‌توان، به شرط آنكه در ابتدا ماتريس‌ها توسط يك تبديل مناسب به صورت خطي تغيير يابند، ضريب همبستگي ميان عناصر دو ماتريس را محاسبه نمود. در نتيجه سطح معني‌دار ضريب مانتل همان سطح ضريب استاندارد شده خواهد بود. اين محاسبات توسط كامپيوتر انجام مي‌گيرد و نرم‌افزار NTSYS- pc يكي از نرم‌افزارهاي مورد استفاده براي انجام اين محاسبات است (Sokal and Rohlf. 1995).

 در مطالعه‌اي كه به منظور بررسي تنوع ژنتيكي و خويشاوندي دوگونه Bromus با استفاده از نشانگرهاي RAPD, AFLP انجام شد، همبستگي بين دندروگرام‌هاي بدست آمده و از هر دو تكنيك با استفاده از آزمون مانتل مورد ارزيابي قرار گرفت. در اين تحقيق نشان داده شد كه بين ماتريس‌هاي كوفنتيك^[6] حاصل از داده‌هاي ALFP , RAPD همبستگي بالاي)9/0 (r= وجود دارد. علاوه بر اين در تحقيق فوق، اين آزمون براي مقايسه بين نتايج حاصل از ماتريس فاصله و دندروگرام‌هاي مربوطه در هر تكنيك نيز بطور جداگانه انجام شد و ميزان همبستگي بالايي را كه نشان‌دهنده صحت دندروگرام‌هاي رسم شده بود، نشان داد (Ferdinandez and Coulman. 2002).

[1] Hadamard product

[2] Randomization test

[3] Permutation

[4] Arbitraty unit

[5] Product- moment correlation

[6] Cophenetic matrixes